Difference between revisions of "Projects:DTIModeling"
| Line 21: | Line 21: | ||
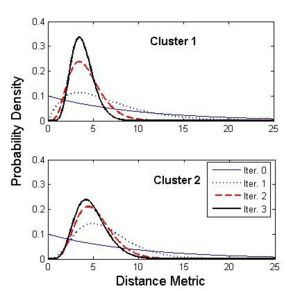
Figure below illustrates the evolution of the Gamma distribution for the clusters of the first case shown the above figure. Convergence is achieved just after a few iterations of the EM algorithm. | Figure below illustrates the evolution of the Gamma distribution for the clusters of the first case shown the above figure. Convergence is achieved just after a few iterations of the EM algorithm. | ||
| − | [[Image: | + | [[Image:Gamma.jpg|300px]] |
| + | |||
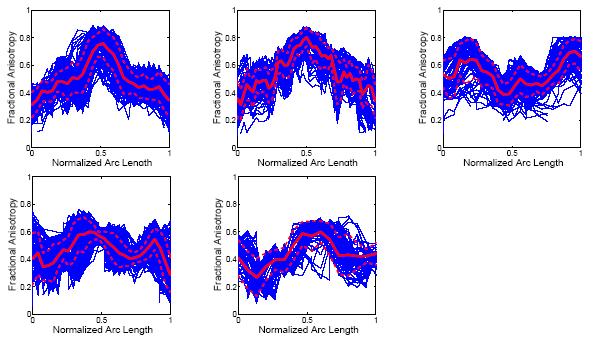
An example of tract-based quantitative analysis is shown below for five bundles of fiber tracts. The FA is plotted vs. the arc length. Note that since the point correspondance between the trajectories is already known with our clustering algorithm, no further aligining is needed for performing quantitative analysis along the tracts. | An example of tract-based quantitative analysis is shown below for five bundles of fiber tracts. The FA is plotted vs. the arc length. Note that since the point correspondance between the trajectories is already known with our clustering algorithm, no further aligining is needed for performing quantitative analysis along the tracts. | ||
Revision as of 14:52, 25 April 2007
Home < Projects:DTIModelingDiscription
Collaborators: Mahnaz Maddah, Sandy Wells, Simon Warfield and Eric Grimson.
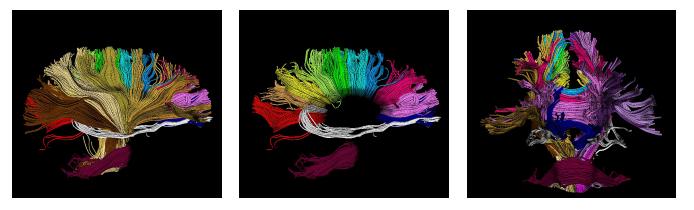
We developed a novel approach for joint clustering and point-by-point mapping of white matter fiber pathways. Knowledge of the point correspondence along the fiber pathways is not only necessary for accurate clustering of the trajectories into fiber bundles, but also crucial for any tract-oriented quantitative analysis.
We employ an expectation-maximization (EM) algorithm to cluster the trajectories in a Gamma mixture model context. The result of clustering is the probabilistic assignment of the fiber trajectories to each cluster and an estimate of the cluster parameters, i.e. spatial mean and variance, and point correspondences. The fiber bundles are modeled by the mean trajectory and its spatial variation. Point-by-point correspondence of the trajectories within a bundle is obtained by constructing a distance map and a label map from each cluster center at every iteration of the EM algorithm. This offers a time-efficient alternative to pairwise curve matching of all trajectories with respect to each cluster center.
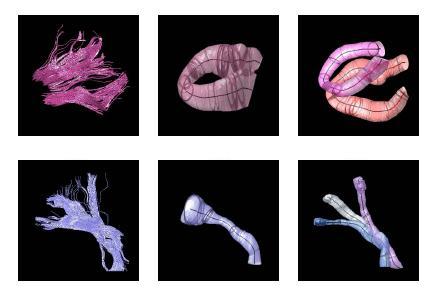
The proposed method has the potential to benefit from an anatomical atlas of fiber tracts by incorporating it as prior information in the EM algorithm. The algorithm is also capable of handling outliers in a principled way. Here are some examples of modeling/clustering the bundles:
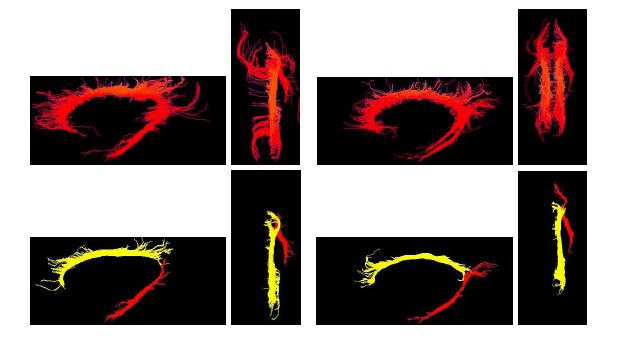
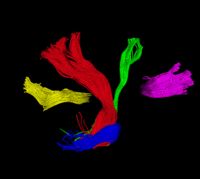
One of the difficult bundles of fiber tracts to cluster is the cingulum. Even starting tractography from a user-defined ROI results in a set of disordered trajectories, mostly short in length because of low FA. Also, due to its adjacency to the corpus callosum, many callosal trajectories are included that adversely affect any further analysis of the bundle. As shown in the following figure for two subjects, our method is well capable of clustering these trajectories into the desired bundles. Two arbitrary trajectories, one from the the superior and one from the posterior part of the cingulum were selected as the initial cluster centers. Knowledge of the point correspondence and hence rigorous calculation of the similarity measure is essential for clustering of such a disordered set of trajectories.
Figure below illustrates the evolution of the Gamma distribution for the clusters of the first case shown the above figure. Convergence is achieved just after a few iterations of the EM algorithm.
An example of tract-based quantitative analysis is shown below for five bundles of fiber tracts. The FA is plotted vs. the arc length. Note that since the point correspondance between the trajectories is already known with our clustering algorithm, no further aligining is needed for performing quantitative analysis along the tracts.
Publications
[1] M. Maddah, W. M. Wells, S. K. Warfield, C.-F. Westin, and W. E. L. Grimson, Probabilistic Clustering and Quantitative Analysis of White Matter Fiber Tracts,IPMI 2007, Netherlands.
[2] M. Maddah, S. K. Warfield, W. E. L. Grimson, W. M. Wells, A Unified Framework for Clustering and Quantitative Analysis of White Matter Fiber Tracts, Accepted for publication in Medical Image Analysis.
[3] M. Maddah, W. M. Wells, S. K. Warfield, C-F. Westin, and W. E. L. Grimson, A Spatial Model of White Matter Fiber Tracts to be presented at ISMRM 2007, Berlin.
[4] M. Maddah, W. E. L. Grimson, and S. Warfield, Statistical Modeling and EM Clustering of White Matter Fiber Tracts 3rd IEEE International Symposium on Biomedical Imaging: Macro to Nano (ISBI) 2006, pp. 53-56.
[5] D. Goldberg-Zimring, A. U. J. Mewes, M. Maddah, S. K. Warfield, Diffusion Tensor Magnetic Resonance Imaging in Multiple Sclerosis J Neuroimaging, vol. 15, pp. 68S-81S, 2005.
[6] M. Maddah, A. Mewes, S. Haker, W. E. L. Grimson, and S. Warfield, Automated Atlas-Based Clustering of White Matter Fiber Tracts from DTMRI. MICCAI05, Palm Spring, CA, pp. 188-195, 2005.
Software
Currently, all of the codes are implemented in MATLAB.