Inter-slice Motion Correction for fMRI
From NAMIC Wiki
Home < Inter-slice Motion Correction for fMRI
Contents
Objective
* To perform inter-slice motion correction in fMR images using affine and non-rigid registration methods.
Progress
* Implemented and tested b-Spline/affine registration with Mattes-MI and KL metrics. * Coding completed. However, results are far from satisfactory. * Progress (maybe) stymied by "poor" resolution of data. * Progress (maybe) stymied by "not-so-viable" metrics (MI, etc.).
Algorithms Used From ITK
Metrics
- Mean Squared - smooth, and for rigid registration, the minimum is fairly correct (physically)
- MI (Wells, Mattes) - very non-smooth - lot of discontinuities. For all motions, results are wrong (possibly because cannot identify a good minimum pt)
- KL-Divergence (Chung, Wells, et. al.) - again very non-smooth. Cannot identify a good minimum point.
Transformations
- Rigid - works well for ms metric
- Affine - does not work for any metric
- B-spline non-rigid - tested with ms and kl. Extremely poor results.
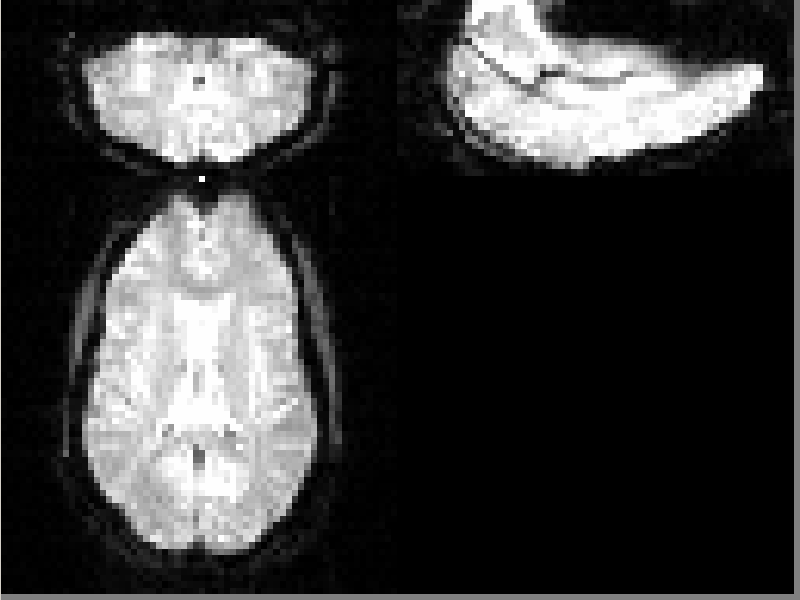
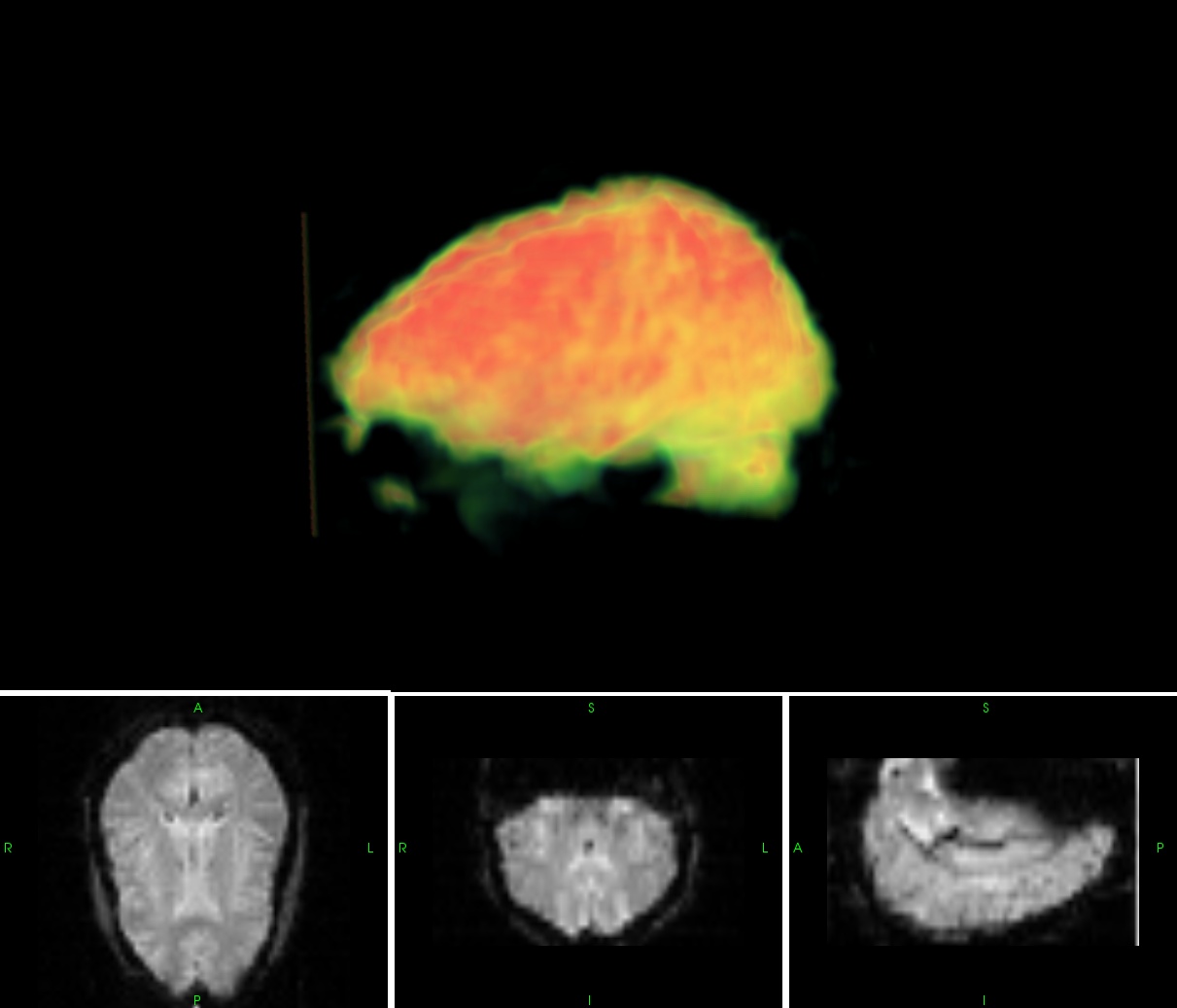
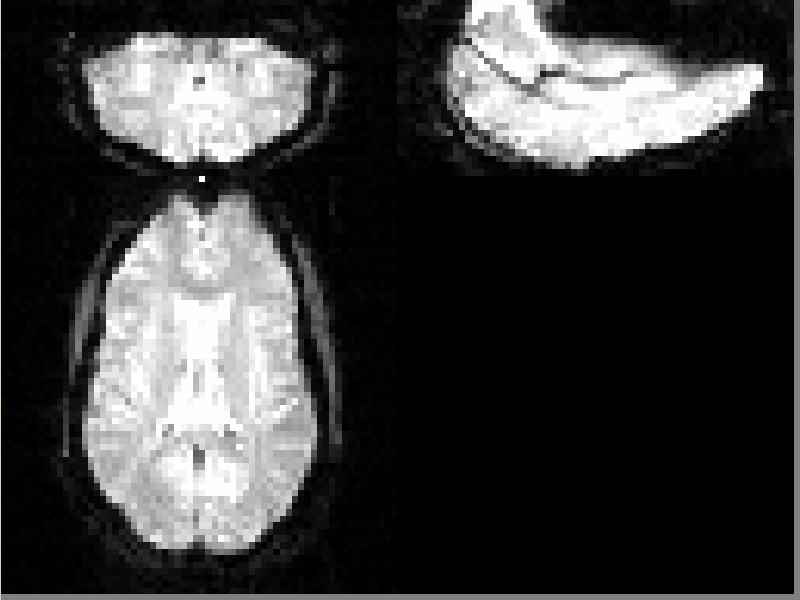
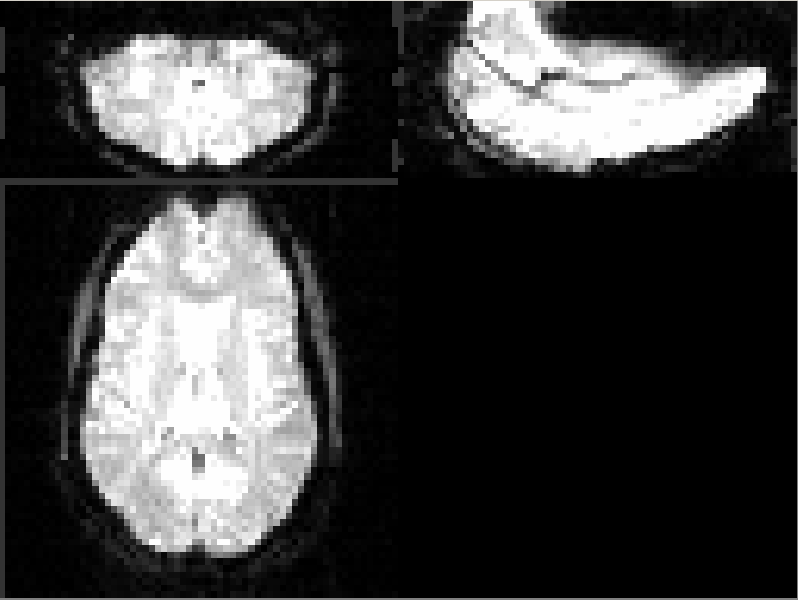
Results
Original fMRI
MS Metric with Rigid Motion
MS Metric with Affine Transform
Mattes MI metric with rigid transform
Mattes MI metric with affine transform
Issues
- As can be seen any registration result looks more jagged (along the sagittal and coronal sections).
- Low sampling rate and image noise - all the metrics are extremely non-smooth as a result.
- Even the slightest change in initialization results in a large deviation in the registration result.
Open questions
* Intensity normalization / histogram equalization - would these have any impact on inter-slice registration? Would they affect the computation of the joint-entropies for MI/KL metrics. * Should there be some regularization factor on the registration to limit the motion ?
To Do
* Right now, registration is done on a slice by slice basis. However, due to the low resolution of fMRI and the absence of gradients result in low registration accuracy. We are investigating using alternative image-to-image metrics like the KL divergence. We are also looking at simultaneously registering multiple slices.
Key Investigators
* Firdaus Janoos, Raghu Machiraju, Steve Pieper, Wendy Plesniak.