Difference between revisions of "Projects:TumorModeling"
| Line 25: | Line 25: | ||
| − | |||
We propose a joint generative model of tumor growth and of image observation that naturally handles multi-modal and longitudinal data. We use the model for analyzing imaging data in patients with glioma. The tumor growth model is based on a Fisher-Kolmogorov reaction-diffusion framework. Model personalization relies only on a forward model for the growth process and on image likelihood. We take advantage of an adaptive sparse grid approximation for efficient inference via Markov Chain Monte Carlo sampling. The approach can be used for integrating information from different multi-modal imaging protocols and can easily be adapted to other tumor growth models. | We propose a joint generative model of tumor growth and of image observation that naturally handles multi-modal and longitudinal data. We use the model for analyzing imaging data in patients with glioma. The tumor growth model is based on a Fisher-Kolmogorov reaction-diffusion framework. Model personalization relies only on a forward model for the growth process and on image likelihood. We take advantage of an adaptive sparse grid approximation for efficient inference via Markov Chain Monte Carlo sampling. The approach can be used for integrating information from different multi-modal imaging protocols and can easily be adapted to other tumor growth models. | ||
| Line 34: | Line 33: | ||
{| | {| | ||
| + | |[[Image:fisher-state-space_tumor-shapes.png|thumb|left|300px| Figure 3: Variation of tumor shapes for different parameterizations of the Fisher-Kolmogorov tumor model. All tumors have the same size, they vary in Diffusivity 'D' and proliferation 'rho'. In our approach this shape information is used to infer general properties of the tumor.]] | ||
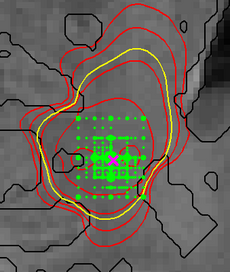
| [[Image:Sampling_spatial-parameters.png|thumb|left|230px| Figure 4: Adaptive grid sampling of the parameter space for a modeled tumor. Green dots show sampling points. Red and yellow lines show isolines of tumor cell infiltration. (Also see text above.)]] | | [[Image:Sampling_spatial-parameters.png|thumb|left|230px| Figure 4: Adaptive grid sampling of the parameter space for a modeled tumor. Green dots show sampling points. Red and yellow lines show isolines of tumor cell infiltration. (Also see text above.)]] | ||
| + | |- | ||
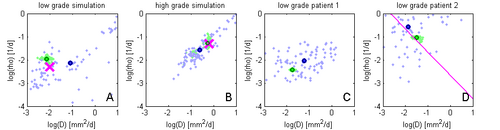
|[[Image:Results_Tumor-Model.png|thumb|left|500px| Figure 5: MCMC sampling results for 'D' and 'rho' using different synthetic and real data sets. The proposed method (green samples) shows less variation when compared to the standard sampling approach (blue) and is at least as close to the ground truth (pink). (Also see text above.) ]] | |[[Image:Results_Tumor-Model.png|thumb|left|500px| Figure 5: MCMC sampling results for 'D' and 'rho' using different synthetic and real data sets. The proposed method (green samples) shows less variation when compared to the standard sampling approach (blue) and is at least as close to the ground truth (pink). (Also see text above.) ]] | ||
|} | |} | ||
Revision as of 04:15, 2 April 2011
Home < Projects:TumorModelingBack to NA-MIC Collaborations, MIT Algorithms
Modeling tumor growth in patients with glioma
We are interested in developing computational methods for the assimilation of magnetic resonance image data into physiological models of glioma - the most frequent primary brain tumor - for a patient-adaptive modeling of tumor growth.
This aims at two directions: First, it aims at making complex information from longitudinal multi-modal data set accessible for diagnostic radiology through physiological models. This will allow us to estimate features such as degree of infiltration, speed of growth, or mass effect in a quantitative fashion; for therapy it will allow us to identify regions at risk for progression. Second, it aims at providing the means to test different macroscopic tumor models from theoretical biology on real clinical data.
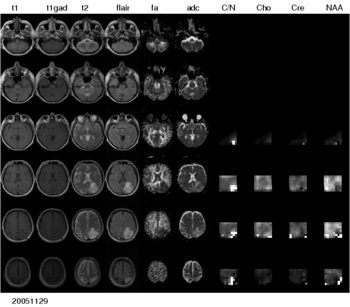
The project has three main aims: 1) the automated segmentation of tumors in large multi-modal image data sets to make information of different MR image modalities accessible for the tumor model, 2) the development of methods for the image-based estimation of parameters in reaction-diffusion type models of tumor growth, and 3) the processing and analysis of magnetic resonance spectroscopic images (MRSI) as a potential application of the tumor model.
Tumor segmentation in large multimodal data sets
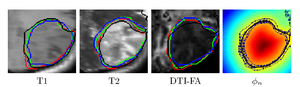
To segment all MR image volumes available for a patient we developed an approach for learning patient-specific lesion atlases (Figure 2) with limited user interaction. Figure 2 shows the manual segmentation of the tumor from different raters (red, green, blue) and the automatic segmentation using the patient-specific lesion atlas (black) in T1-MRI, T1-MRI and the fractional anisotropy map from DTI.
Image-based modeling of tumor growth
We propose a joint generative model of tumor growth and of image observation that naturally handles multi-modal and longitudinal data. We use the model for analyzing imaging data in patients with glioma. The tumor growth model is based on a Fisher-Kolmogorov reaction-diffusion framework. Model personalization relies only on a forward model for the growth process and on image likelihood. We take advantage of an adaptive sparse grid approximation for efficient inference via Markov Chain Monte Carlo sampling. The approach can be used for integrating information from different multi-modal imaging protocols and can easily be adapted to other tumor growth models.
Figure 4 illustrates the adaptive grid sampling of the parameter space for a modeled tumor. The size of the green sampling points indicates how often the indicated location parameter of the tumor model was evaluated under different parametrizations. The ground truth is indicated by the pink cross. Most adaptively chosen sampling points are close to the ground truth. The figure also shows isolines of tumor cell density (red), the predicted extensions of the T2 hyper-intense area (yellow) and tissue boundaries (black).
Figure 5 shows results of the proposed approach: Green samples are obtained from the proposed sparse grid approach while blue sample are obtained via standard MCMC. Black circles indicate means of the two distributions. Ground truth for A and B are indicated by the pink cross. In D the previously estimated speed of growth [7] is shown by the pink line. The sparse grid sampling approximation performs better than the direct MCMC (A-B). Estimates correlate well with priviously published results, but provide a more accurate characterization of the state of disease (D).
Processing magnetic resonance spectroscopic images
To make the metabolic information of magnetic resonance spectroscopic images available for modeling the evolution of glioma growth we are implementing an MRSI processing module for Slicer jointly with the SIVIC project at UCSF.
We envision that physiological tumor models may be used to interpret MRSI, integrating the highly specific metabolic information of the spectroscopic images with other clinical MRI modalities in a principled fashion.
Key Investigators
- MIT: Bjoern Menze, Tammy Riklin Raviv, Koen Van Leemput, Polina Golland
- Harvard: William M. Wells
- INRIA Sophia-Antipolis, France: Ezequiel Geremia, Olivier Clatz, Nicholas Ayache
- Microsoft Research, UK: Ender Konukoglu
- DKFZ Heidelberg, Germany: Bram Stieltjes, Marc-Andre Weber