2010 Summer Project Week SegmentationMeshEmbeddedContours
Surface Mean Curvature
Converged Contour Surrounding Region
Initial Points From User
Segmenting Tibia Fracture via Surface Geometry
Key Investigators
- Georgia Tech: Peter Karasev, Karol Chudy, Allen Tannenbaum
- BWH: Ron Kikinis
Update
1. Setup Slicer4 "superbuild", verified module consistency therein
2. Signed up for ITK write access as there is some partial overlap and functions in this module perform tasks that ITK doesn't do:
i. large neighborhood curvature computation via paraboloid fit ii. unstructured graph sparse field level sets )
3.
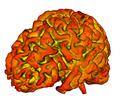
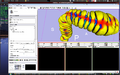
4. Curvature overlay in Slicer:
surface curvature display inside slicer (vtkFloatArray attached to returned vtkPolyData)
5. Implemented a helpful re-factor, convert a beefy struct with bunch of global functions to a class with member functions plus non-member non-friend helper functions in anonymous namespace
/* NEW */
namespace {
TestFunc1( const MeshData& data ) { ... }
}
class MeshData{
public:
functionA( );
functionB( );
...
}
/* OLD */
struct MeshData{
member1;
member2;
....
}
functionA( MeshData* ) { ... }
functionB( MeshData* ) { ... }
...
6. Learn about and setup qtcreator, continue development of stand-alone frontend and module there (it blows Eclipse away for C/C++)
Module development in QT Creator (in Ubuntu Linux 9.10)
Objective
We are developing methods for segmentation of surfaces defined by polygonal meshes. In image or volume-slice segmentation, 'information' comes from image intensity, while in mesh surface segmentation the information is purely geometric. The goal of this project is to develop algorithms allowing a user to quickly and robustly segment one or several regions on a surface. Specifically, it is required to reconcile some concepts in classical differential geometry and embedded curves with the numerical and discrete-space constraints of polygon meshes.
Approach, Plan
Our approach for analyzing surface-embedded segmentation is separated into two parts. First, the notion of surface geometry for a polygonal mesh must be suitably defined. To this end, we study numerically stable and robust methods of estimating the geometry of the surface (mean curvature, tangent plane bases, second fundamental form, etc) and that of the segmenting curve. Second, we explore definitions of functionals whose extrema lead to useful geometric flows on the surface. The techniques for these two tasks must always consider the difficulty imposed by data purely in the form of a polygon mesh. This project makes extensive use of the VTK library to simplify data storage, communication, and visualization.
Our plan for the project week is to first come up with the best encapsulation framework for data storage and persistence, making the existing Slicer3 implementation feature-complete. Secondly, we seek to explore reformulation of existing image volume segmentation and mesh generation such that the numerical stability and accuracy of subsequent surface segmentation is taken into consideration.
Progress
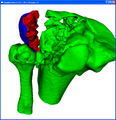
A version of this software exists in Slicer3, with a standalone version being updated to encapsulate the functionality as a vtkPolyDataFilter. It has been experimentally verified to give useful segmentation results for meshes involving bone fractures (separating smooth non-fracture surface from jagged break zone). Some of the robustness issues (mesh connectivity, neighborhood sizes, differentiable basis functions) that have been seen to make a user experience inconsistent have been formulated as mathematical problems, allowing provable algorithm improvements to move forward.
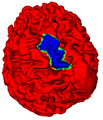
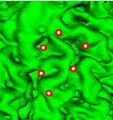
At the moment, the modules documentation and code can be found at the it's relative Slicer Documentation page.[1]. Using a series of data structures and algorithms outlined below, we calculate the best fit curve that encapsulates all of the users self-chosen fiducial points. Through a series of iterations in our closed-path algorithm, we continuously select vertices that are equidistant from existing path points and add them to our path data structure. By running this algorithm until our path, and therefore segmentation selection, consists of a closed group of points, we can highlight a region with as little as 3 points after enough iterations. Once the path is closed we can select all of the points inside of it and add them to our selection data structure.
To obtain consistent results we smooth out our 'organic blob' of points through a series of iterations, trying to minimize the total curvature of the closed path. This makes it so that our selection doesn't stop in the middle of say, a ridge or bump, but will encapsulate what the user is most likely trying to segment.
Currently the module is implemented correctly and is fairly robust. We are looking at perhaps adding some extra features and increasing efficiency, especially with larger data sets. Because of the way we calculate the closed path, the larger the desired selection, the calculation required by our algorithm increases exponentially.
Previous Notes:
As part of the restructuring effort, a data structure outline of the internals of the module has been made. It makes obvious some aspects that should be refactored.
Current Internal Data Structures of Module
However the internals are functional, so it was decided that the priority is the *external* interface, which should look like a pipeline of vtkPolyDataAlgorithms, as shown below.
Pipeline of vtkPolyDataAlgorithm subclasses encapsulating module internals.
The result is that the module code SparseFieldLevelSetContour.cxx used to interface with the module goes from including 8 header files and having access to low-level implementation details to including only one header. The included header contains a namespace with non-member non-friend functions with overloaded entry points to the module.
The module pipeline now contains three classes that extend vtkPolyDataAlgorithm. It now makes use of vtkSmartPointer.
- vtkInitClosedPath : take in poly data and set of fiducial points, create a closed path including the closest points on the mesh to the given fiducials. Searches for pre-existence of geometry information, pass-through if it already exists.
- vtkComputeLocalGeometry : take in poly data, compute curvature, its derivatives, and related differential geometric quantities. Uses its own version of curvature computation- vtk versions are not useable because they only consider 1-neighborhood. Searches for pre-existence of geometry information, pass-through if it already exists.
- vtkLevelSetMeshEvolver : take in poly data with a scalar array defining the current region boundaries. Update the boundaries with curve evolution and return poly data with updated scalar array.
Development is much easier now for two reasons:
1. After the reformulation of external interface, the standalone application which can be built easily in windows has virtually identical interface to the module as the Slicer CLI entry point. This allows rapid development in the standalone demo in windows to be copied directly to Slicer in linux.
2. Much improved knowledge of linux development, particularly being able to execute the various scripts for Slicer without doing getbuildtest.tcl; saves time.
The namespace:
namespace MeshContourEvolver {
// Input: mesh and indices of vertices for initialization
vtkPolyData* entry_main( vtkPolyData* inputMesh, const vector<int>& initPointVertexIndices );
// Input: mesh and 3D points for initialization. This is what you get
// when inputting 'fiducials' in Slicer GUI. The 3D points
// are not on the mesh, you need to first find closest points on the mesh.
vtkPolyData* entry_main( vtkPolyData* inputMesh, const vector< vector<float> >& initPoints3D );
// Input: mesh only. No initialization of points; either continue
// evolution of existing curve or only pre-compute geometry!
vtkPolyData* entry_main( vtkPolyData* inputMesh );
}
The pipeline code; e.g. external interface. Functionality is encapsulated in the vtkPolyDataAlgorithm subclasses.
// Input: mesh and indices of vertices for initialization
vtkPolyData* MeshContourEvolver::entry_main( vtkPolyData* inputMesh,
const vector<int>& initPointVertexIndices )
{
// instantiate output mesh
vtkPolyData* outputMesh = vtkPolyData::New();
// algorithm #1: initialization of path
vtkSmartPointer<vtkInitClosedPath> initPath = vtkSmartPointer<vtkInitClosedPath>::New();
initPath->SetInput( inputMesh );
// algorithm #2: computing the geometry (if the input data
// does NOT already have a scalar data set containing it)
vtkSmartPointer<vtkComputeLocalGeometry> computeGeometry = vtkSmartPointer<vtkComputeLocalGeometry>::New();
computeGeometry->SetInputConnection( initPath->GetOutputPort() );
// algorithm #3: run curve evolution and update the scalar dataset for display
vtkSmartPointer<vtkLevelSetMeshEvolver> evolver = vtkSmartPointer<vtkLevelSetMeshEvolver>::New();
evolver->SetInputConnection( computeGeometry->GetOutputPort() );
evolver->Update();
// register and return the result of the pipeline of algorithms
vtkSmartPointer<vtkPolyData> result = evolver->GetOutput();
outputMesh->DeepCopy( result );
return outputMesh;
}
References
P.A. Karasev, J.G. Malcolm, M. Niethammer, R. Kikinis, A. Tannenbaum. User-Driven 3D Mesh Region Targeting. SPIE Medical Imaging 2010.
