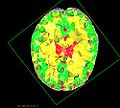
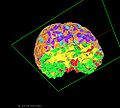
Tissue Dependent Registration
Key Investigators
- Petter Risholm (PhD Student, Harvard Medical School (BWH), University of Oslo)
- William Wells (Professor, Harvard Medical School (BWH) )
Objective
Most registration methods treat tissue parameters as uniform parameters over the image domain. For instance, when brain tissue is modeled as an elastic material, identical stiffness parameters are used for all tissue types (CSF, GM, WM). In our approach, we let each tissue type take on varying stiffness parameters and solve for the deformation as well as the stiffness parameters at the same time.
We pose the elastic registration problem as a Bayesian problem where we marginalize out the elastic parameters. A Markov Chain Monte Carlo (MCMC) sampling technique is applied to characterize the posterior. However, even though the elastic parameters are marginalized out, we can retain the elastic samples and also characterize the distribution of the elastic parameters.
We use a linear elastic Finite Element (FE) model to compute the likelihood (similarity term) and the deformation prior (regularizer). In a FE registration model, tissue is modeled by a mesh. To accurately model the tissue and let elastic parameters vary according to tissue type, we require a tissue dependent tetrahedral mesh. Assuming we have a segmentation of the brain tissue into CSF, GM and WM, we need a mesh where the tetrahedra conform to the different tissue types (the edges of a tetrahedra do not cross from one tissue type to the other but are either fully within a tissue type or on the boundary between two tissue types).
To properly characterize the posterior with a MCMC approach, a large number of samples is often needed. The FE-computations are the bottleneck as the FE-system has to be constructed and computed for each new sample generated. Hence, it is necessary with fast FE computations to generate enough samples.
Approach, Plan
Generate tissue dependent tetrahedral meshes.
Optimize FE-computations.