2012 Summer Project Week:NiftyReg

• 

  Projects List

• 

  NiftyReg

What is Niftyreg?

• Light-weight package for medical image registration.
• Global (rigid/affine) registration based on a block-matching technique.
• Local deformation (non-rigid) based on a cubic B-Spline parametrisation.
• Implementation: C/C++ [SIMD, OpenMP, CUDA]
• All dependencies are included into the project (nifticlib, zlib, [NRRD, png]).
• Installation through CMake and step-by-step install can be found here
• Trunk can be downloaded through svn: svn co https://niftyreg.svn.sourceforge.net/svnroot/niftyreg/trunk/nifty_reg niftyreg

Key Investigators

• University College London: Marc Modat
• BWH: Sonia Pujol

Objective

NiftyReg is an open-source package for rigid, affine and non-linear registration developed the team of Dr. Sebastien Ourselin at the Centre for Medical Imaging Computing, University College London, UK. The objectives is to make NiftyReg available in Slicer.

Approach, Plan

Our approach is to develop a CLI module for NiftyReg in Slicer4.

Progress

• The NRRD file format have been integrated into the NiftyReg package to ease its integration.
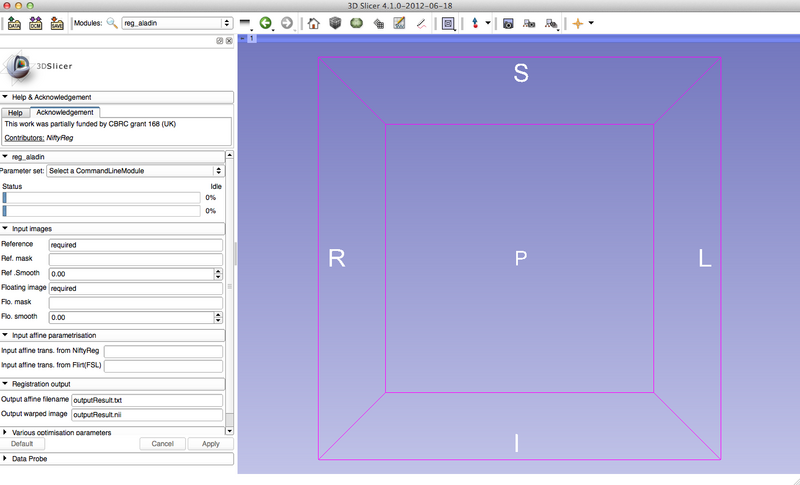
• The XML file for one of the executable of NiftyReg: reg_aladin has been created and the slicer module created.
• reg_aladin is the global registration tool from NiftyReg. It is based on a block-matching approach to establish correspondences and a trimmed least square optimisation to determine the robust global transformation.
• The project CMake organisation has been altered to enable easy integration of the other executables.

Reg_aladin Module screenshot

References

• Modat et al. Fast free-form deformation using graphics processing units. Comput Meth Prog Bio (2010) vol. 98 (3) pp. 278-84
• Daga et al. Accurate Localisation of Optic Radiation during Neurosurgery in an Interventional MRI Suite. IEEE Transactions on Medical Imaging (2012)
• Modat. Parametric non-rigid registration using a stationary velocity field. Mathematical Methods in Biomedical Image Analysis (MMBIA), 2012 IEEE Workshop on (2012) pp. 145 - 150