Algorithm:Past Featured Articles
Back to NA-MIC Algorithms
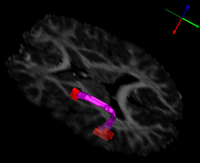
- Fletcher et al.. "Microstructural Connectivity of the Arcuate Fasciculus in Adolescents with
High-functioning Autism"
| The arcuate fasciculus is a white matter fiber bundle of great importance in language. In this study, diffusion tensor imaging (DTI) was used to infer white matter integrity in the arcuate fasciculi of a group of subjects with high-functioning autism and a control group matched for age, handedness, IQ, and head size. The arcuate fasciculus for each subject was automatically extracted from the imaging data using a new volumetric DTI segmentation algorithm. The results showed a significant increase in mean diffusivity (MD) in the autism group, due mostly to an increase in the radial diffusivity (RD). A test of the lateralization of DTI measurements showed that both MD and fractional anisotropy (FA) were less lateralized in the autism group. These results suggest that white matter microstructure in the arcuate fasciculus is affected in autism and that the language specialization apparent in the left arcuate of healthy subjects is not as evident in autism, which may be related to poorer language functioning. | |
| "Microstructural Connectivity of the Arcuate Fasciculus in Adolescents with
High-functioning Autism", P.T. Fletcher, R.T. Whitaker, Ran Tao, Molly B. DuBray, A. Froehlich, C. Ravichandran, A.L. Alexander, E. D. Bigler, N. Lange, J.E. Lainhart To appear, Neuroimage, 2010 |
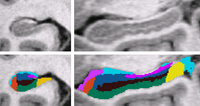
- K. Van Leemput, et al. Bayesian Segmentation of MRI Images for Hippocampus
| We use a Bayesian modeling approach for image segmentation, in which we build a parametric computational model of how an MRI image around the hippocampal area is generated. The model incorporates a prior distribution that makes predictions about where neuroanatomical labels typically occur throughout the image, and is based on a generalization of probabilistic atlases that uses a deformable, compact tetrahedral mesh representation. The model also includes a likelihood distribution that predicts how a label image, where each voxel is assigned a unique neuroanatomical label, translates into an MRI image, where each voxel has an intensity.
Given an image to be segmented, we first estimate the parameters of the model that are most probable in light of the data. The parameter estimation involves finding the deformation that optimally warps the mesh-based probabilistic atlas onto the image under study, as well as finding the mean intensity and the intensity variance for each of the hippocampal subfields. Once these parameters are estimated, the most probable image segmentation is obtained. | |
| Automated Segmentation of Hippocampal Subfields from Ultra-High Resolution In Vivo MRI, K. Van Leemput, A. Bakkour, T. Benner, G. Wiggins, L.L. Wald, J. Augustinack, B.C. Dickerson, P. Golland, and B. Fischl. Hippocampus. Accepted for Publication, 2009. |
| This paper presents a novel multiscale shape representation and segmentation algorithm based on the spherical wavelet transform. This work is motivated by the need to compactly and accurately encode variations at multiple scales in the shape representation in order to drive the segmentation and shape analysis of deep brain structures, such as the caudate nucleus or the hippocampus. Our proposed shape representation can be optimized to compactly encode shape variations in a population at the needed scale and spatial locations, enabling the construction of more descriptive, nonglobal, nonuniform shape probability priors to be included in the segmentation and shape analysis framework. In particular, this representation addresses the shortcomings of techniques that learn a global shape prior at a single scale of analysis and cannot represent fine, local variations in a population of shapes in the presence of a limited dataset.
Specifically, our technique defines a multiscale parametric model of surfaces belonging to the same population using a compact set of spherical wavelets targeted to that population. We further refine the shape representation by separating into groups wavelet coefficients that describe independent global and/or local biological variations in the population, using spectral graph partitioning. We then learn a prior probability distribution induced over each group to explicitly encode these variations at different scales and spatial locations. Based on this representation, we derive a parametric active surface evolution using the multiscale prior coefficients as parameters for our optimization procedure to naturally include the prior for segmentation. Additionally, the optimization method can be applied in a coarse-to-fine manner. We apply our algorithm to two different brain structures, the caudate nucleus and the hippocampus, of interest in the study of schizophrenia. We show: 1) a reconstruction task of a test set to validate the expressiveness of our multiscale prior and 2) a segmentation task. In the reconstruction task, our results show that for a given training set size, our algorithm significantly improves the approximation of shapes in a testing set over the Point Distribution Model, which tends to oversmooth data. In the segmentation task, our validation shows our algorithm is computationally efficient and outperforms the Active Shape Model algorithm, by capturing finer shape details. | |
| D. Nain, S. Haker, A. Bobick, A. Tannenbaum, Multiscale 3-D Shape Representation and Segmentation Using Spherical Wavelets . IEEE Transactions on Medical Imaging, 26(4):598-618, 2007. |
- K. M. Pohl et al. A Bayesian Model for Joint Segmentation and Registration
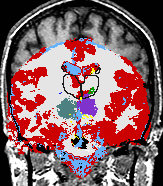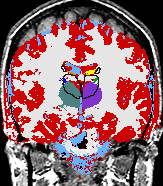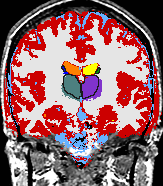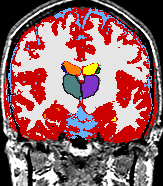
|
A statistical model is presented that combines the registration of an atlas with the segmentation of magnetic resonance images. We use an Expectation Maximization-based algorithm to find a solution within the model, which simultaneously estimates image artifacts, anatomical labelmaps, and a structure-dependent hierarchical mapping from the atlas to the image space. The algorithm produces segmentations for brain tissues as well as their substructures. We demonstrate the approach on a set of 22 magnetic resonance images. On this set of images, the new approach performs significantly better than similar methods which sequentially apply registration and segmentation. |
| K. M. Pohl, J. Fisher, W.E.L. Grimson, R. Kikinis, and W.M. Wells, A Bayesian Model for Joint Segmentation and Registration. NeuroImage, 31(1):228-239, 2006. |