Projects:ShapeAnalysisWithOvercompleteWavelets
Back to MIT Algorithms
Shape Analysis with Overcomplete Wavelets
In this work, we extend the Euclidean wavelets to the sphere. The resulting over-complete spherical wavelets are invariant to the rotation of the spherical image parameterization. We apply the over-complete spherical wavelet to cortical folding development and show significantly consistent results as well as improved sensitivity compared with the previously used bi-orthogonal spherical wavelet. In particular, we are able to detect developmental asymmetry in the left and right hemispheres.
Description
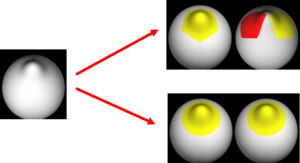
Bi-orthogonal spherical wavelets have been shown to be powerful tools in the segmentation and shape analysis of 2D closed surfaces, but unfortunately they suffer from aliasing problems and are therefore not invariant under rotations of the underlying surface parameterization. See the toy example in the figure below.
Instead, we propose to use the over-complete spherical wavelets. These over-complete spherical wavelets are based on filter bank theory, directly extending the ideas of Euclidean steerable pyramid to the sphere. We demonstrate the theoretical advantage of over-complete wavelets over bi-orthogonal wavelets. We also show that over-complete spherical wavelets allow us to build more stable cortical folding development models, and detect a wider array of regions of folding development in a newborn dataset. The use of spherical wavelet transform in cortical shape analysis allows us to study cortical folds of different spatial scales, which are difficult to analyze by cortical folding analysis methods based on local features such as curvature and sulcal depth measurements.
Experimental Results
Comparison with Bi-orthogonal Wavelets
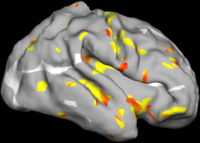
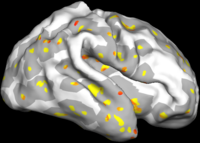
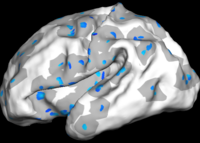
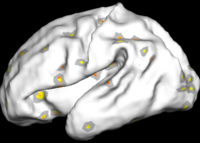
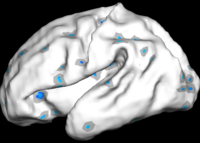
The two images on the left of the figure below show the cortical folding speed detected by the bi-orthogonal wavelets. Notice, how the detection changes wildly with different parameterizations. On the other hand, the results of over-complete wavelets are stable across different parameterizations. Furthermore, the over-complete wavelets are much more sensitive than the bi-orthogonal wavelets in detecting changes.
Overcomplete Wavelets Global Shape Analysis
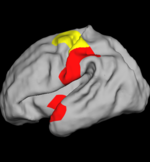
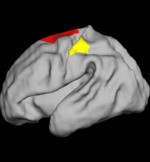
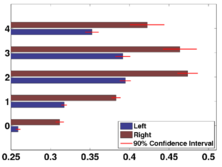
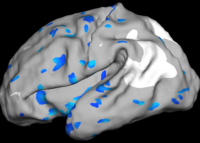
As seen in the figure below, we find that larger folds (lower wavelet scales) develop earlier but slower. This is consistent with the previous postmortem study[3]. Furthermore, we find that the fastest folding development occurs at a younger age on the left hemisphere than on the right.
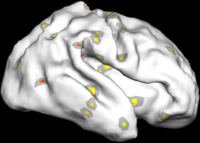
Overcomplete Wavelets Local Shape Analysis
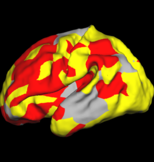
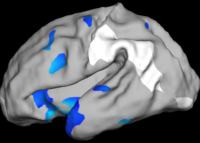
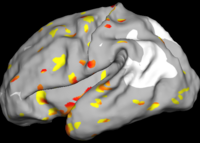
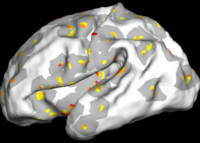
The figure below shows the results of the regional analysis. Consistent with the global development result discussed above, regions that develop earlier (darker blue) also grow more slowly (more red). For example, the lateral side of the parietal lobe on the left hemisphere develops earlier than the right hemisphere, but at a slower speed.
Also consistent with the global analysis, we find that larger folds develop earlier but slower. On the lateral side, the pre- and post-central gyri develop the fastest during 30-31 weeks on both hemispheres while smaller structures such as supramarginal and angular gyri develop the fastest at a much later time, as indicated at frequency level 3.
|
Maximum Growth Rate (Left) |
Maximum Growth Rate (Right) |
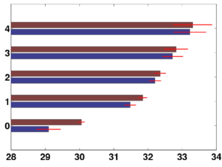
Age of Maximum Growth (Left) |
Age of Maximum Growth (Right) |
Key Investigators
- MIT: [| B.T. Thomas Yeo], Peng Yu, Wanmei Ou, Polina Golland.
- Harvard: Ellent Grant, Bruce Fischl.
Publications
NA-MIC Publications Database on Shape Analysis With Overcomplete Wavelets